For software engineers, especially those without a background in computer science, the term "Big O Notation" has come to be terrifying. I always made an effort to stay away from discussions, articles, and other Big O-related material, but I was doing more harm than good to myself because, as a software developer, you need to know the difference between good and bad code, the trade-offs between the data structures and algorithms you want to use when structuring or building your programs, and how to optimize your code to be better. You can do that by using Big O Notation.

What is Big O Notation? Big O Notation (Big O asymptotic analysis) is a metric used to describe the efficiency of an algorithm. It is used to evaluate the speed and efficiency of various data structures. It explains why one data structure should be chosen over another. Big O notation is used to determine what is a good and bad solution to a problem. Before discussing Big O Notation, you should first understand what a good code is and why it is necessary for developers to have good codes.

Good code is a code that is:

• Readable
• Scalable

Scalable is concerned about speed and memory.

Speed: How fast is our runtime on the code? How much time does it take for a function to run? How many operations does it cost? That is the time complexity. Time complexity is a way to show how the runtime of a function increases as the size of the input increases.

Memory: When we talk about memory, we mean the space complexity. Space complexity is concerned about the additional space to be taken and not the space already taken up by the inputs. Space complexity is the same as time complexity, the only thing that changes is the question asked. How does the space usage scale as input gets very large?

How much does our algorithm slow down as we increase the size of our input? The less it slows down, the better.

Let us discuss code efficiency.

There are various methods for storing information. Big O notation was created by programmers as a way to score different data structures based on the following criteria:

• The ability to access specific elements within the data structure
• Searching for a specific element within the data structure
• Inserting an element into the data structure
• Removal of a data structure element

The efficiency of an algorithm mostly depends on:

• Running time

The running time of an algorithm depends on the size (n) of the input, where n is an arbitrary number.

• Memory

How does the efficiency of a function scale with increase in input size? Big O is focsed on how quickly the runtime grows.

Different notations in Big O

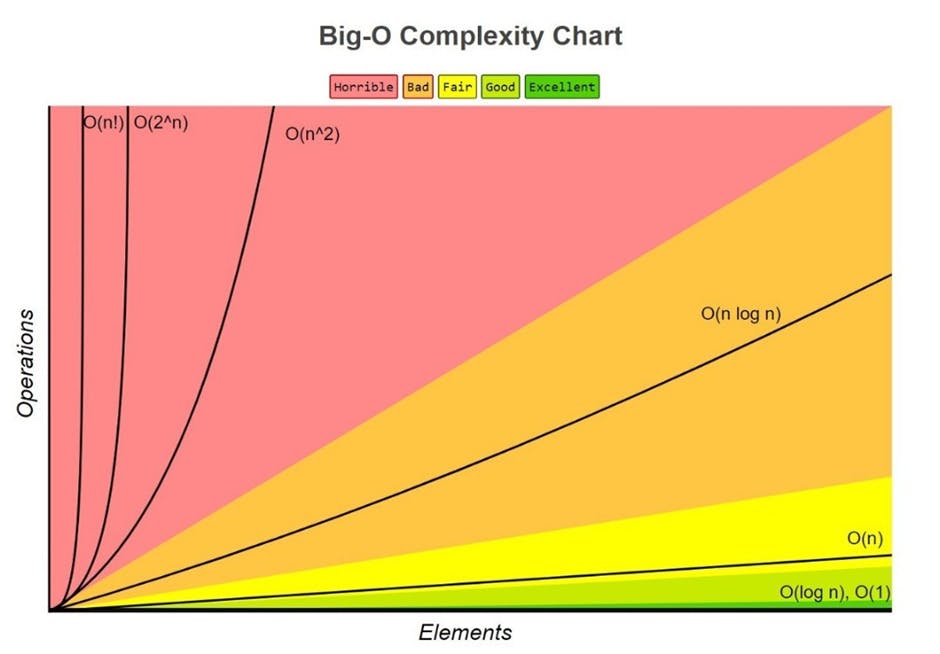
O(1) - Constant time; this is the absolute best a data structure can score. No matter the size of the dataset or input, the algorithm will be completed in one step or one operation. Examples are:

• accessing elements in an indexed array
• push operations (adding an element to the end of an array)
• pop operations (removing an element from the end of an array)

let nums = [1, 2, 3, 4, 5]

O(log n) - The second fastest type of time complexity equation. It gets more efficient as the size of the data increases. It's called Logarithmic algorithm. Example include divide and conquer algorithm using binary search.

O(n) - Linear time; This is the next common time complexity equation. For every element added to the dataset, the amount of operations needed to complete the function will increase by the same amount. As the number of inputs increase, number of operations increases in linear time. (10 elements, 10 steps, 20 elements, 20 steps). Examples are:

• linear search (Finding an element within an array)
• Insertion and deletion operations

let nums = [];
for (let i = 0; i < 100; i++) {
    nums[i] = i + 1;
}
console.log(nums);

O(n^2) - Quadratic time; This means that the number of operations it performs grows in proportion to the square of the input. This is very bad in terms of efficiency as the runtime slows down with increase in input size resulting from the algorithm whose growth doubles with increase to the input. Examples are:

• Sorting algoritms

I would stop here for now and cover the other Big O Notations much later.

You should note that worst case scenerios are always used when judging data structures. Big O notation is the language we use for talking about how long an algorithm takes to run. When we talk about Big O and scalability of code, we simply mean when we grow bigger and bigger with our input, how much does the algorithm or function slow down? The less it slows down, the better.